Metode Newton Raphson, Algoritma dan Source Code

Hello sobat blogger, maaf kemarin ane gak ngepost, maklum sibuk, sempet ada MA UKKI PENS. Setelah kemarin saya ngepos tentang metode biseksi, iterasi dan regula falsi, kali say mau ngepos tentang metode Newton Raphson. Sebernanya seperti apa sih metode Newton Raphson itu? Metode Newton Raphson adalah salah satu metode numerik yang digunakan untuk mencari kar dari suatu persamaan kuadrat dengan pendekatan yang menggunakan satu titik awal dan mendekatinya dengan memperhatikan gradien pada titik tersebut.

Beriku adalah algoritma metode Newton Raphson :

1.  Definisikan fungsi x(f(x) dan turunan fungsi x (g(x));   
2.  Masukan nilai awal x, toleransi error, dan jumlah iterasi;
3. Inisialisasi i =0;
4.  fx[i] = fungsi(x[i]);
5.  gx[i] = tururan f(x[i])
6.  abso[i] = fx[i];
7.  jika fx[i]<0 data-blogger-escaped-abso="" data-blogger-escaped-i="" data-blogger-escaped-span="">
8.  Cetak nilai x[i], fx[i], gx[];
9.  i++;
10.  Jika abso[i] kurang dari e (toleransi error) atau i kurang dari jumlah iterasi;
11.  Ya : Keluar perulangan;
12.  Tidak : kembali ke 4.

Berikut adalah listing Metode Newton Raphson

#include

#include

double fungsix(double);

double diffungsix(double);

main(){

      double x[20]={0}, fx[20], gx[20], e=0.0001,abso[20]; //gx merupakan turunan fx

      int i =0, n=9;

      puts("\t\t>>>>>>>METODE NEWTON RAPSON<<<<<<<");

      puts("\t\t\t  f(x)=x+e^x");

      puts("=================================================================");

      printf("Masukan nilai x        : ");

      scanf("%lf", &x);

      printf("Masukan nilai error    : ");

      scanf("%lf", &e);

      printf("Masukan jumlah iterasi : ");

      scanf("%d", &n);

      puts("=================================================================");

      printf("| n |      x       |       fx     |     gx       |  absolut fx  |\n");

      puts("=================================================================");

     

      while(i<=n){

            fx[i] = fungsix(x[i]);

            gx[i] = diffungsix(x[i]);

            x[i+1]= x[i] - (fx[i]/gx[i]);

            abso[i] = fx[i];

            if(abso[i]<0 data-blogger-escaped-span="">

                  abso[i] *=-1;

            printf("|%2d | %12.9lf | %12.9lf | %12.9lf | %12.9lf |\n",i+1, x[i], fx[i],gx[i],abso[i]);

           

            if(abso[i] < e)

                  break;

           

            i++;

      }

      puts("=================================================================");

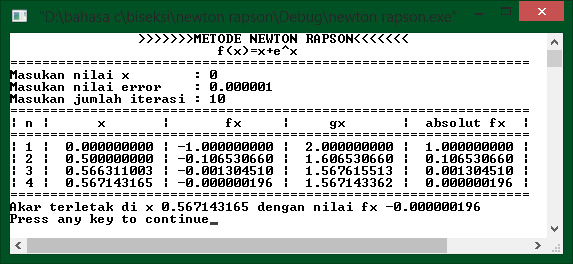
      printf("Akar terletak di x %9.9lf dengan nilai fx %9.9lf\n",x[i], fx[i]);

}

double fungsix (double a){

      double hasil;

      hasil = a - exp(-a); //bisa diganti sesuai yang dingingankan

      return hasil;

}

double diffungsix (double b){

      double hasil2;

      hasil2 = 1 + exp(-b); //merupakan turunan fungsi fx

      return hasil2;

}

terimakasih sobat bloger yang sudah berkunjung, berbagi itu menyenangkan.
sekian untuk pos hari ini.

sekilas motivasi : "Kesalahan terbesar yang di buat manusia di dalam kehidupannya adalah terus-menerus mempunyai rasa takut bahwa mereka akan membuat kesalahan."~Elbert HUbart

Artikel Terkait c ,metode numerik ,tutorial